Difference between revisions of "Modus Tollens"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
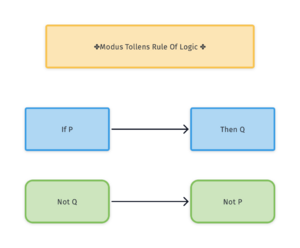
Consider the rule of logic known as modus tollens, also known as denying the consequent. This rule states that If P, then Q. Not Q. Therefore, not P. Here is a simple example: If a shape is a triangle (P), then it has three sides (Q). The figure does not have three sides (not Q). Therefore it is not a triangle (not P). | Consider the rule of logic known as modus tollens, also known as denying the consequent. This rule states that If P, then Q. Not Q. Therefore, not P. Here is a simple example: If a shape is a triangle (P), then it has three sides (Q). The figure does not have three sides (not Q). Therefore it is not a triangle (not P). | ||
| + | |||
| + | [[File:Modus Tollens diagram.png|thumb]] | ||
Latest revision as of 15:51, 21 April 2020
Consider the rule of logic known as modus tollens, also known as denying the consequent. This rule states that If P, then Q. Not Q. Therefore, not P. Here is a simple example: If a shape is a triangle (P), then it has three sides (Q). The figure does not have three sides (not Q). Therefore it is not a triangle (not P).