Difference between revisions of "Chicago Skyline"
(→Expert) |
|||
| Line 8: | Line 8: | ||
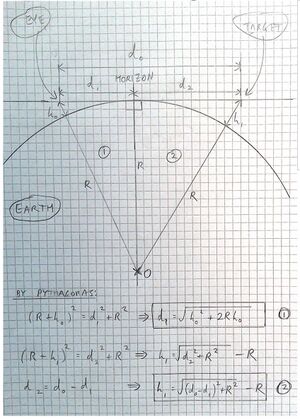
We can use the Pythagorean Theorem to determine the rate at which objects should disappear in the distance if we lived on a globe-shaped object of the dimensions claimed. The Pythagorean Theorem states that in a right triangle with hypotenuse c and legs a and b, the following equivalency holds: a^2 + b^2 = c^2. Therefore, c = sqrt (a^2 + b^2). | We can use the Pythagorean Theorem to determine the rate at which objects should disappear in the distance if we lived on a globe-shaped object of the dimensions claimed. The Pythagorean Theorem states that in a right triangle with hypotenuse c and legs a and b, the following equivalency holds: a^2 + b^2 = c^2. Therefore, c = sqrt (a^2 + b^2). | ||
| − | [[File: | + | [[File:UsingPythagoreanTheorem.jpg|thumb]] |
==Expert== | ==Expert== | ||
Revision as of 14:52, 6 April 2020
Contents
Beginner
One of the primary claims regarding the reality that our earth measures flat is that "We see too far." What does this mean? Because we are given a supposed measurement for the radius of the earth, according to the official globe model, we can use math to calculate at what rate objects should disappear in the distance behind this imaginary curvature. The important thing to remember is that this alleged curvature is never actually measured or seen. There are however, countless observations made of distant objects that would be hidden from view if the earth really were a sphere with a radius of 3959 miles. Many observations and photographs of the Chicago Skyline across Lake Michigan are at distances of over 50 miles, an impossibility on a globe of the size claimed.
Advanced
We can use the Pythagorean Theorem to determine the rate at which objects should disappear in the distance if we lived on a globe-shaped object of the dimensions claimed. The Pythagorean Theorem states that in a right triangle with hypotenuse c and legs a and b, the following equivalency holds: a^2 + b^2 = c^2. Therefore, c = sqrt (a^2 + b^2).
Expert
Refraction